机器学习笔记

机器学习期末知识点总结

第一讲：基本概念

1. 什么是机器学习?
   • 机器学习就是指计算机算法能够像人一样，从数据中找到信息，从而学习一些规律，也就是“利用经验来改善系统自身的性能”。
2. 什么是监督学习?
   • 机器学习中的监督学习，主要是指须对用于训练学习模型的样本进行人工标注或打标签，即须事先通过人工方式把数据分成不同的类别。通俗地说，先拿已经分好类的样本对机器学习模型（如神经网络）进行训练，确定模型参数（连接权值和偏置等），然后把待分类的新样本输入经过训练的模型中进行分类。
3. 什么是迁移学习?
   • 迁移学习（Transfer Learning, TL）是指利用数据、任务或模型之间的相似性，将在旧领域学习过的模型应用于新领域的一种学习过程。

第二讲：神经元与线性回归梯度下降

1. 脑神经元有哪四个部分组成?
   • 细胞体、树突、轴突、突触。（此题为常识题）
2. 计算题：梯度下降法求解线性回归
   • 直线形式为 y = ax + b，初始化令 a = 1, b = 1，设置学习率 lr = 0.1。
   • 给定 3 个样本点 (x, y) = (0, 0.52)、(1, 1.12)、(2, 2)。训练 2 轮（即 2 次参数更新），写出得到的直线与计算过程。本题为计算题，需给出计算过程。

第三讲：支持向量机（SVM）

1. 用自己的语言，说明 SVM 的基本原理
   • SVM 是一种有监督的线性分类模型，利用带类别标签的数据进行训练，预测新数据的类别标签。SVM 的输入数据是向量形式，希望找到一个超平面，将不同标签的向量分开。每一类训练数据中，距离超平面最近的向量被称为“支持向量”，SVM 的训练是使得支持向量到超平面的距离之和最大。
2. 写出 SVM 的基本型公式
   • $\arg\min\limits_{w,b} \frac{1}{2}\lVert w\rVert^2$
     s.t. $(w^\top x + b)y \ge 1$。
   • 
   • 

第四讲：朴素贝叶斯与 AdaBoost

1. 用自己的语言，简述朴素贝叶斯分类器的基本原理
   • 朴素贝叶斯分类器是一种基于贝叶斯定理的分类方法，其核心思想是计算后验。根据训练数据统计每个类别出现的概率，作为类别的先验。对于每个类别，基于特征独立性假设，将各特征的条件概率相乘，得到样本在该类别下的联合概率。将联合概率与对应类别的先验概率相乘，计算样本属于各类别的后验概率。比较所有类别的后验概率大小，选择后验概率最大的类别作为分类结果。
   • 贝叶斯公式：$P(y\mid x) = \frac{P(x\mid y)P(y)}{P(x)} = \frac{P(x\mid y)P(y)}{\sum_y P(x\mid y)P(y)}$；特征独立时 $P(x\mid y)=\prod_i P(x_i\mid y)$。
   • 
2. 用自己的语言，简述 AdaBoost 算法的基本原理
   • AdaBoost 是一种集成学习方法，认为样本具有权重。1) 初始时，所有样本具有同样的权重；2) 用所有样本训练一个弱分类器；3) 使用得到的弱分类器对训练样本进行分类；4) 将分错的样本权重增加；5) 重复 2-4 过程，每次可以得到一个弱分类器，最终将所有分类器的结果加权。

第五讲：人工神经元与网络类别

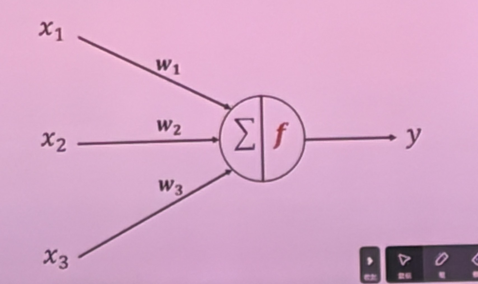
1. 描述人工神经元的原理，并画出其结构
   • 神经元接受多个输入信号，根据权重加权求和，与阈值比较之后通过激活函数，得到输出。当激活函数为 sgn 时，如果加权和大于阈值则输出 1，否则输出 0。（画图可用等价形式）
   • 
2. 神经网络按拓扑结构、信息流向、学习方式的分类
   • 拓扑结构：层次型结构、互连型结构。
   • 信息流向：前馈型网络、反馈型网络。
   • 学习方式：有监督学习（监督学习、有导师学习）、无监督学习（无导师学习）、灌输学习。
3. 设计一个单层感知机并指定参数以实现逻辑 OR，写出其参数，并给出其对 OR 真值表的测试过程
   • 答案不唯一。

第六讲：多层感知器与激活函数

1. 多层感知器与单层感知器的相同、不同之处
   • 相同：都是对向量的变换，基本原理一致，每一层都是多输入求加权和，再通过激活函数。
   • 不同：多层感知器具有隐藏层，能够解决线性不可分问题。
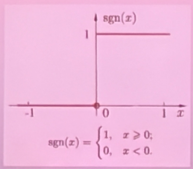
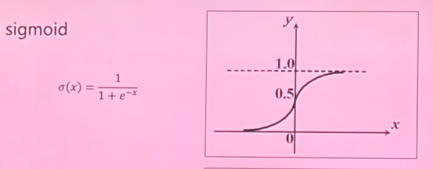
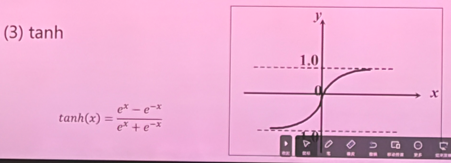
2. 写出以下激活函数的表达式，并画出函数图像
   • 符号函数 sgn(x)。
   • 
   • Sigmoid：$\sigma(x)=\frac{1}{1+e^{-x}}$。
   • 
   • Tanh：$\tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$。
   • 
3. 按照感知器学习规则，以如下设置训练单层感知器一个 epoch（计算题）
   • 学习率 lr = 1；初始值：$w_1 = w_2 = w_3 = 1$。
   • 正样本：(0.8, 0.5, 0)、(0.9, 0.7, 0.3)、(1, 0.8, 0.5)。
   • 负样本：(0, 0.2, 0.3)、(0.2, 0.1, 1.3)、(0.2, 0.7, 0.8)。
   • 本题为计算题，共 6 个样本，包含 6 个 step，需逐样本按规则计算 y、更新权重。

第七讲：反向传播

1. 简述反向传播算法的核心思想
   • 信息正向传播、误差反向传播，通过动态规划算法基于链式法则计算梯度。
2. 可能的改进方向
   • 1. 增加动量项。
   • 1. 自适应调节学习率。
   • 1. 引入陡度因子。
3. 计算题：画出下列表达式的计算图，对样本 (x = 2, w = 1, b = 2) 求梯度
   • $L = f(x) = (wx - b)^2 + w^2$。
   • 拆解运算：$u_1 = wx$，$u_2 = u_1 - b$，$u_3 = u_2^2$，$u_4 = w^2$，$L = u_3 + u_4$。
   • 按计算图求各节点的微分，得到 $\partial L/\partial w$、$\partial L/\partial b$。

第八讲：玻尔兹曼机与模拟退火

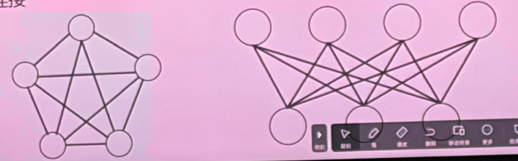
1. 玻尔兹曼机与受限玻尔兹曼机有什么不同? 画出它们各自的网络结构
   • 在 BM 中，所有的节点之间都有连接；在 RBM 中，只有隐藏层和可见层之间具有连接。
   • 
2. 什么是模拟退火方法?
   • 系统一开始有较高的T,随着系统更新，T逐步下降
   • 即系统一开始有较高的温度，具备更强的随机性；随着运行时间增加，确定性增强。

第九讲：深度生成模型

1. 2006 年，Hinton 等人成功训练了一种生成式深度神经网络，开启了深度学习时代。这种网络是
   • 深度置信网络/深度信念网络（DBN）。
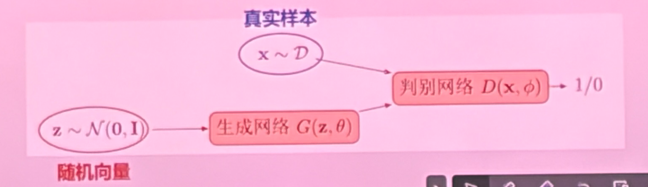
2. 在生成式对抗网络中，判别器的作用是
   • 负责判断生成器生成的样本的真实性，以促进生成器能力的提升。
   • 

第十讲：卷积神经网络

1. 用自己的语言，描述 CNN 的基本原理
   • CNN 对图像的低级特征进行提取，随着网络层数的加深，将低级特征不断地向高级特征映射，适合网格数据。
2. 计算题：有一个 224x224 的输入，使用大小为 5x5 的卷积核进行卷积，卷积核的步长 stride = 2，图像边缘填充 padding = 3，输出的尺寸是多少?
   • 输出尺寸 113x113。
3. 计算题：对给定的输入矩阵 Input，采用卷积核 Kernel 进行卷积运算（stride = 1，padding = 0），画出计算得到的特征图 Feature map，并写出计算过程。

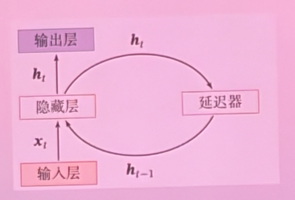
第十一讲：循环神经网络

1. 画出简单 RNN 的结构图，并用自己的语言描述其基本原理
   • 简单 RNN 具有一个输入层、一个隐藏层、一个输出层。每个时刻，隐藏层会同时接收当前的输入与上一时刻的隐藏层输出（延迟器）并进行序列建模。
   • 
2. LSTM 的设计是受到了人脑的什么启发
   • 长时记忆与短时记忆。
3. LSTM 与简单 RNN 相比有什么改进? 其提出是为了解决什么问题
   • 相比于简单 RNN，LSTM 显式增加了长时记忆，并且通过“门控”的方式，是为了解决长时依赖问题。